die Erde mit Atmosphäre

Die Erde mit Atmosphäre

Auf der Seite "Die Erde mit Albedo" habe ich das einfachste Klimamodell, welches das Erde-Sonne-System als Strahlungsbilanz zweier Schwarzer Strahler beschreibt, um die Albedo erweitert. Nun kommen zwei weitere Faktoren dazu: die Atmosphäre und deren begrenztes Absorptionsvermögen. Das Modell basiert auf der Annahme, dass eine wolkenlose Atmosphäre für die Sonnenstrahlung nahezu transparent ist, sodass diese Strahlung die Erdoberfläche uneingeschränkt erreichen kann (Stull, 2017). Für Infrarotstrahlung, die von der Erde ausgestrahlt wird, ist die Atmosphäre hingegen nicht transparent (Stull, 2017). Gase wie Wasserdampf und CO₂ absorbieren einen Teil dieser Strahlung, jedoch nicht alles. Durch die Absorption hat die Atmosphäre eine Temperatur und strahlt entsprechend Infrarotstrahlung aus. Ein Teil dieser Strahlung geht ins All, der andere Teil geht zur Erdoberfläche. Die Erde empfängt also Strahlung sowohl von der Sonne als auch von der Atmosphäre. Wie unten gezeigt wird, ist die Temperatur an der Erdoberfläche deswegen höher als ohne Atmosphäre. Dies ist ein natürlicher Prozess: der sogenannte Treibhauseffekt (Stull, 2017).

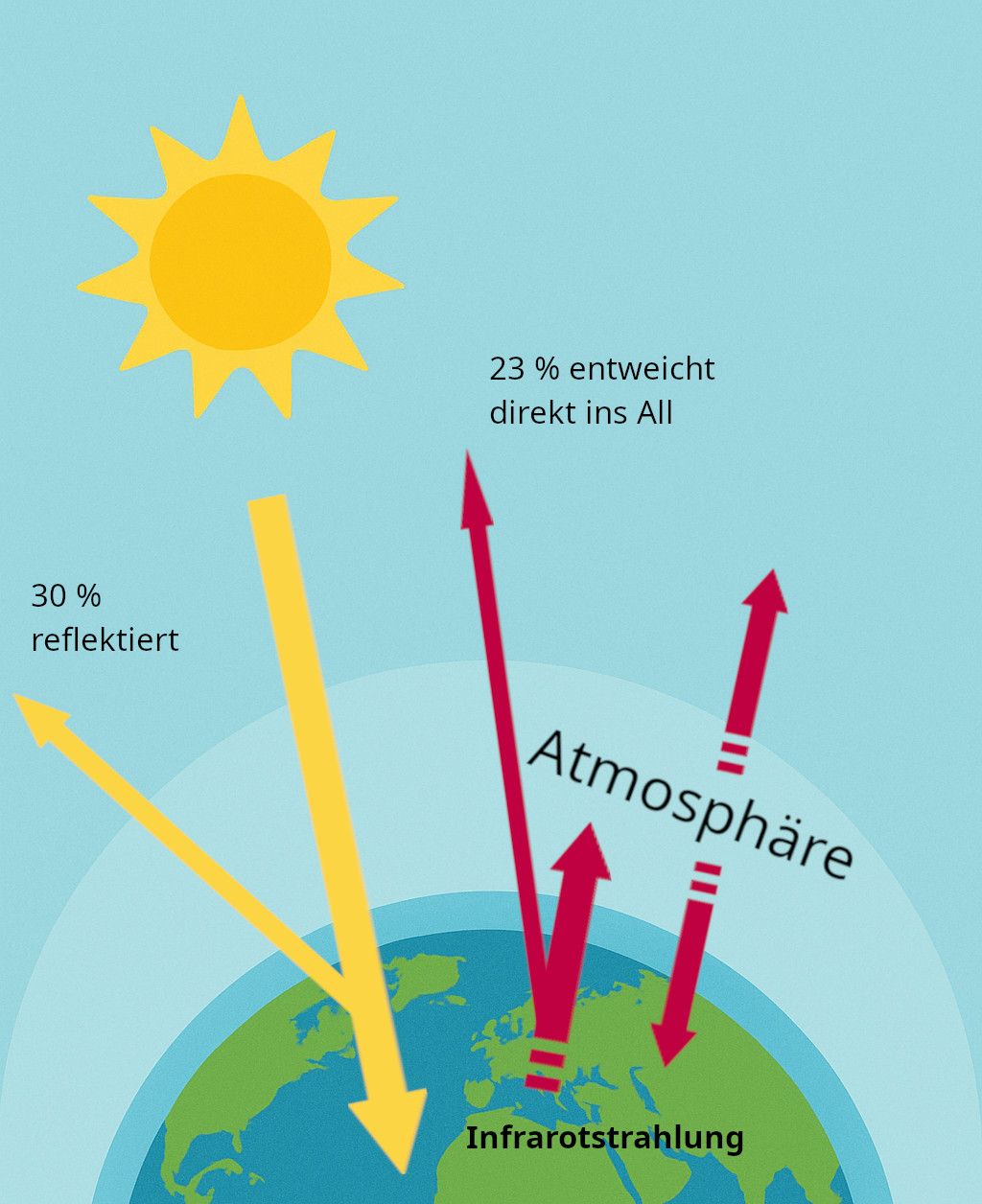
Abbildung 1 zeigt eine vereinfachte Darstellung des Treibhauseffekts. Die Sonnenstrahlung fallt auf die Erde und wird absorbiert, 30 % wird reflektiert. Die Erde strahlt Infrarotstrahlung aus, die für 23 % direkt ins All entweicht und sonst von der Atmosphäre absorbiert wird. Die Atmosphäre wiederum strahlt auch Infrarotstrahlung aus, davon 50 % zur Erdoberfläche und 50 % ins All.

Abbildung 1: Vereinfachte Darstellung des Treibhauseffekts. Die Erde empfängt sowohl Infrarotstrahlung von der Atmosphäre als auch Sonnenstrahlung und ist entsprechend wärmer als ohne Atmosphäre.

Nach dem Kirchhoffschen Strahlungsgesetz gleicht der Absorptionsgrad dem Emissionsgrad (Stull, 2017). Er beschreibt, wie viel Strahlung ein Objekt im Vergleich zu einem idealen schwarzen Strahler absorbieren und ausstrahlen (emittieren) kann. Ein schwarzer Strahler hat eine Emissivität von 1 (100 %), ein transparentes Objekt eine Emissivität von 0. Für die Atmosphäre liegt der Wert bei etwa 0,77 (siehe unten). Um die Strahlungsleistung der Erde und ihrer Atmosphäre korrekt modellieren zu können, muss in der Stefan-Boltzmann-Gleichung die Emissivität berücksichtigt werden (Stull, 2017):

P = O · e σ {(T + 273,15)}^{4}

mit
P - der Strahlungsleistung in W (Watt)
O - der Oberfläche in m²
e - der Emissivität, das Verhältnis der abgestrahlten Energie im Vergleich zu einem schwarzen Körper
σ - der Stefan-Boltzmann-Konstante ≈ 5,67·10^-8 W m^-2K^-4
T - der Temperatur in °C

Modellbeschreibung

Mit dieser Modellerweiterung betrachten wir die Energiebilanz der Erde unter Einbeziehung einer sehr vereinfachten Atmosphäre, wo die Temperatur in jeder Höhe gleich ist. Dabei gibt es zwei Punkte zu berücksichtigen. Erstens, an der Oberseite der Atmosphäre, also dort wo die Strahlung ins All abgegeben wird, gilt: Die Gesamtenergie der einfallenden Sonnenstrahlung entspricht die Summe der Strahlung, die die Erde und die Atmosphäre gemeinsam ins All ausstrahlen (Stull, 2017). Beachte, dass etwa 77 % der Strahlung der Erde durch die Atmosphäre absorbiert wird und entsprechend nicht direkt ins All verschwindet. Somit ergibt sich folgende Gleichung (Stull, 2017):

\frac{{D_{S}}^{2} \cdot σ {(T_{S} + 273,15)}^{4}}{d^{2}} \cdot 0,25 (1 - α) = (1 - e) σ {(T_{E} + 273,15)}^{4} + e σ {(T_{A} + 273,15)}^{4}

mit
α - der Albedo, das Verhältnis der reflektierten Sonnenstrahlung zur einfallenden Strahlung
T_E - der Erdtemperatur in °C
T_A - der Temperatur der Atmosphäre in °C
T_S - der Temperatur der Sonne in °C (= 5498,85 °C)
D_S - dem Durchmesser der Sonne in m (≈ 1.3914·10⁹ m)
d - dem doppelten Abstand zwischen Sonne und Erde in m (2 AU ≈ 2,992·10¹¹ m) (Williams, 2025). Zur mathematischen Vereinfachung wurde die Erdoberfläche, πD_E², mit der alle Komponenten multipliziert werden müsste, hier weggelassen.

Zweitens, am Erdboden gilt: Die Erde emittiert Infrarotstrahlung, deren Gesamtenergie der Summe aus der einfallenden Sonnenstrahlung und der von der Atmosphäre zur Oberfläche gerichteten Infrarotstrahlung entspricht (Stull, 2017). Das bedeutet, sie ist nicht ausschließlich das Ergebnis der einfallenden Sonnenstrahlung, sondern sie hängt auch wesentlich von der atmosphärische Strahlung ab. Somit ergibt sich folgende Gleichung (Stull, 2017):

σ {(T_{E} + 273,15)}^{4} = \frac{{D_{S}}^{2} \cdot σ {(T_{S} + 273,15)}^{4}}{d^{2}} \cdot 0,25 (1 - α) + e σ {(T_{A} + 273,15)}^{4}

Wenn wir nun diese beiden Gleichungen gleichsetzen, erhalten wir eine neue Gleichung, die es uns erlauben wird, die Temperatur der Erde in Bezug auf die Temperatur der Atmosphäre zu berechnen:

σ {(T_{E} + 273,15)}^{4} - e σ (T_{A} + 273,15) = (1 - e) σ {(T_{E} + 273,15)}^{4} + e σ {(T_{A} + 273,15)}^{4}

Daraus ergibt sich, dass (Stull, 2017)

{(T_{E} + 273,15)}^{4} = 2 {(T_{A} + 273,15)}^{4} .

Oder, vereinfacht T_E = 1,1892·(T_A + 273,15) - 273,15.

Die Gleichgewichtstemperatur am Erdboden

Ein Ausdrück für die Gleichgewichtstemperatur am Erdboden ergibt sich, wenn in die erste Gleichung T_A durch T_S substituiert wird (Stull, 2017):

T_{E} = {(\frac{(0,25 \cdot (1 - α))}{(1 - 0,5 e)})}^{\frac{1}{4}} \cdot (T_{S} + 273,15) {(\frac{D_{S}}{d})}^{\frac{1}{2}} - 273,15

Werden die Werte für D_S, d, α und T_E aus den NASA Factsheets (Williams, 2025) verwendet, dann muss für e einen Wert von 0,771 angenommen werden, um mit der obigen Gleichung für T_E die Temperatur von 15,0 °C zu erhalten. Das heißt, laut diesem Modell absorbiert die Atmosphäre etwa 77 % der von der Erde ausgestrahlten Strahlung, während 23 % direkt ins All entweichen. Die Temperatur von 15,0 °C ist um 33 °C höher als die Temperatur von -18,0 °C, die ohne den Treibhauseffekt vorherrschen würde. Die entsprechende, homogene Temperatur der Atmosphäre lässt sich leicht berrechnen (sie Gleichung oben) und ergibt -30,8 °C. Dieses einfache Modell illustriert, wie der Treibhauseffekt die Temperatur am Erdboden über dem Gefrierpunkt hebt, indem die Atmosphäre einen Teil ihrer Strahlung zur Erde ausstrahlt.

Quellen und Literatur:
* Stull R (2017) Practical Meteorology: An Algebra-based Survey of Atmospheric Science -version 1.02b. Univ. of British Columbia. 940 pages. ISBN 978-0-88865-283-6 (https://www.eoas.ubc.ca/books/Practical_Meteorology/index.html).
* Williams DR (2025) NASA Planetary Factsheet, https://nssdc.gsfc.nasa.gov/planetary/factsheet/

Klimasystem